Graph Theory Lessons

Lesson 1: Null Graphs

The simplest type of graph is a null graph. It consists of a non-empty finite set of elements called vertices. The applet below shows some examples of null graphs.

applet 1

We shall use this exercise to introduce you to the program Petersen. If you decide to copy and run this program at home you will need the executable program Petersen.exe and the file vbrun100.dll.

Click on the Petersen icon to start the program. After the welcome message and copyright notice you will get a screen with two rectangles. The large one is for pictures of graphs and the lower one will have instructions and messages. To input a null graph, click on Graph and then Null Graph. You will get an input box with the question "How many vertices (< 66)". The "<66" is there to indicate that the maximum number of vertices that this program will accept is 65. Press 4 and then press the Enter key (or click OK.) You will get four vertices on the screen like in Fig. 1. The N(4) at the top means Null graph on four vertices, sometimes written as N₄.

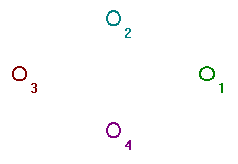
Fig. 1, The Null Graph N₄

In a similar way try to get the null graph with 10 vertices called N₁₀. Notice that the labels 1, 2, 3, etc. are the same color as the vertices they refer to. This will be useful when you have many vertices on the screen. If the colors don't come out well on your monitor you can turn the color off by clicking Picture, Color and then Off. Try a few others like N₂₅ and so on.

Null graphs are not very interesting so let us introduce some edges. These will be line segments from one vertex to another.
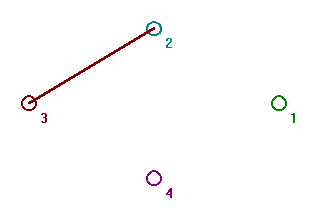
Two vertices v₁ and v₂ are adjacent if there is an edge between them. Use the procedure outlined above and get N₄ on your screen as in Fig. 1. To add an edge from vertex 3 to vertex 2 you click on vertex 3 with the right mouse button and drag to vertex 2. Your graph should now look like Fig. 2.

Fig. 2

Experiment and add edges to graphs as you wish to get used to the program. One thing you will notice is that the graphs are simple graphs (no more than one edge between vertices and no loops). You will also notice that the program always represents edges as straight lines. We shall find that even with these limitations that there are a lot of interesting things we can do. To erase an edge you do the same thing: use the right mouse button and drag from one vertex to the other. Sometimes you will need to store your graph on disk so let us learn how to save and restore a graph. Get the graph N₂₅ as above. To save it click Graph and Save. You will get an input box with instructions "Save as graph [1...9]". Let us save this graph as graph 1. Press 1 and Enter. Now suppose at a later time we want to get this graph from the disk. To restore a file you click Graph and Restore. There are many interesting graphs so let us look at a few of them. They can all be obtained by using the menu labeled "Graph". Complete graphs are graphs in which every vertex is adjacent to every other vertex. Click Graph then Complete then Complete Graph. You will be asked how many vertices you want. Input an integer (e.g. 5). You will then get the complete graph on 5 vertices which we will call K₅ for short. A complete bipartite graph has the vertices in two groups (let us call them the left and right )and all vertices in one group are adjacent to all vertices in the other. If you click Graph then Complete then Complete Bipartite you will be asked to input how many vertices you want on the left and on the right. Try 4 vertices on the left and 3 on the right to get the graph we will call K_4,3. Now that you get the idea I will not spoil the fun -- explore and ask questions if you find anything puzzling!