Graph Theory Lessons
Lesson
2: Handshaking Lemma
The degree of a vertex is the number of
edges incident to it, i.e. the number of edges that have it as an endpoint.
We want to find out how the sum of the degrees of the vertices in a graph
is related to the number of edges in the graph. Start by drawing a few graphs
in the following applet. Check to see that the statistics the applet gives you
are what you think they should be.
Counting edges and degrees
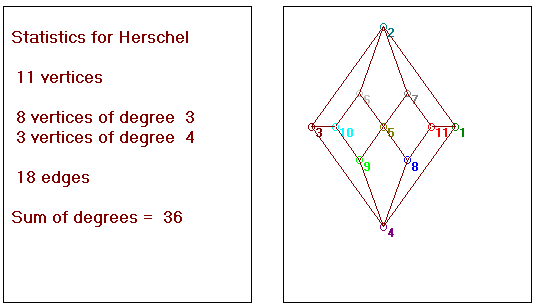
Let us now look at more interesting graphs. Start the Petersen program and
click Graph and Herschel. The graph you get is called the Herschel
graph. Now click Properties and Statistics. You will get
a list of the number of vertices, the degrees of the vertices, and the
number of edges as in Fig. 3.
|
|
Fig. 3, Statistics
for the Herschel Graph
|
A simple graph
is a graph that does not have more than one edge between any two vertices
and no edge starts and ends at the same vertex. Whenever it is not specified
in the exercises assume that we are talking about a simple graph.
Restore graphs 10 through 20 and make a table
showing the sum of the degrees, and the number of edges and another table
showing the number of vertices with odd degree and the number of vertices
with even degree.
| Graph |
Sum of degrees |
Number of edges |
| 10 |
. |
. |
| 11 |
. |
. |
| Graph |
Number of odd degree vertices |
Number of even degree vertices |
| 10 |
. |
. |
| 11 |
. |
. |
-
What do you think the relationship between the sum of degrees and the number
of edges is? Give an argument to support your answer.
-
Is it possible for the sum of degrees to be an odd number? Give a reason
for your answer.
-
Use your answer to part 2 to prove that the number of vertices of odd degree
in a simple graph is always even.
-
Suppose a simple graph has 15 edges, 3 vertices of degree 4, and all others
of degree 3. How many vertices does the graph have?
-
Is it possible to have a group of nine people such that each person is
acquainted with exactly five of the other people? Either draw a graph that
demonstrates this or give a reason why it is not possible.
-
Notice in the statistics that there are always at least two vertices of
whose degrees are equal. Prove that a simple graph on n vertices
where n>1 always has at least two vertices of the same degree.
-
Give an example of a non simple graph with four vertices that has all vertices
of different degree.
e-mail: C. Mawata
© C. Mawata