Graph Theory Lessons

A simple circuit on n vertices, C_n is a connected graph with n vertices x₁, x₂,..., x_n, each of which has degree 2, with x_i adjacent to x_i+1 for i=1,2,...,n-1 and x_n adjacent to x₁. In what follows "circuit" refers to "simple circuit". In the program you can get a circuit by choosing Graph and Circuit. We shall assume that n > 2 in all the questions.

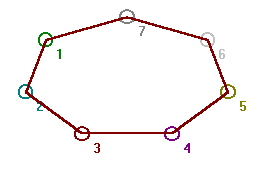
Fig. 16, The graph C7.

1. How many edges does C_n have? (Use the statistics option to investigate a few circuit graphs)
2. Which circuit is a complete graph?
3. Look at the adjacency matrices of a few circuits. Write down the adjacency matrix for C₆.
4. What is the chromatic number of C₇, C₈, C₁₁?
5. In general what is the chromatic number of C_n?
6. For what values of n is C_n bipartite?
7. Is it possible for a bipartite graph to contain a circuit C_n with n odd as a subgraph? Give a reason for your answer.



---

When a graph contains a subgraph isomorphic to C_n we say that it has an n-cycle. We can use the program to check if there is an n-cycle in a graph. Below is a picture showing a 6-cycle in the Petersen graph.

A word of warning: when there is no n-cycle the program could take a long time before it exhausts all possibilities so let us agree that if the program does not find the cycle in 2 min we shall assume there is none. (We shall discuss in class why it takes so long.
8. What is the size of the largest cycle in the Petersen graph?
9. What is the size of the largest cycle in the Herchel graph?

---

A wheel on n vertices, W_n is a graph with n vertices x₁, x₂,..., x_n, x₁ having degree n-1 and all the other vertices having degree 3. The vertex x₁ is adjacent to all the other vertices, and for i=2,...,n-1, x_i is adjacent to x_i+1, and x_n-1 is adjacent to x₂. In the program you can get a wheel by clicking Graph and Wheel . We shall assume that n>3 in all the problems.
 

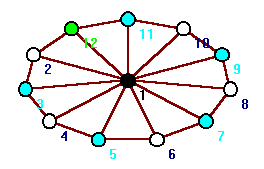
Fig. 17, The graph W12 has chromatic number 4.

10. How many edges does W_n have?
11. Which wheel is a complete graph?
12. Write down the adjacency matrix for W₈.
13. What is the chromatic number of W_n?
14. Is it possible for W_n to be bipartite?

Answers

e-mail: C. Mawata    © C. Mawata