Graph Theory Lessons

An Euler circuit on a graph G is a circuit that visits each vertex of G and uses every edge of G. The applet below displays Euler circuits for complete graphs K_n. You will notice that some graphs do not have Euler circuits.

To answer the questions that follow you will need to use the Petersen program so, as an example, let us use the program to find an Euler circuit in the complete graph K₅. First get K₅ and then select Properties and Euler Circuit. You will see the circuit traced out on the graph. Use the three buttons at the bottom right corner of the screen to speed up or slow down the drawing. When you have seen enough click on the halt button.

1. Which of the complete graphs K_n have Euler circuits?
2. Which of the platonic graphs have Euler circuits?
3. Under what conditions on r and s does the complete bipartite graph Kr,s have an Euler circuit?
4. Under what conditions on r, s, and t does the complete tripartite graph Kr,s,t have an Euler circuit?
5. Does the Petersen graph have an Euler circuit?



---

Theorem: If a simple graph has an Euler circuit then all the vertices have even degree.
6. Consider the statement "If all the vertices of a simple graph have even degree the the graph has an Euler circuit". That statement is the converse of the Theorem. Is it a true statement? Hint: If you can find an example of a simple graph with all vertices of even degree but no Euler circuit you will have shown the converse of the theorem to be false. Such an example is called a counter example.



---

So far we have considered an edge from a vertex v₁ to a vertex v₂ to be the same as an edge from v₂ to v₁. The edge was therefore defined by an unordered pair of vertices. If we want to consider direction, we need to use an ordered pair to define our edges which we will call directed edges. In this case an edge from v₁ to v₂ is different from an edge from v₂ to a vertex v₁. We shall use an arrow to represent the direction. A graph that has directed edges is called a directed graph or sometimes just a digraph. The number of edges that end at a vertex is called the in-degree of the vertex while the number of edges that start at a vertex is the out-degree of the vertex.
7. What relationship do you think there is between the sum of the in-degrees of the vertices of a graph and the sum of the out-degrees ?
Draw a digraph in the left part of the applet below and, if your digraph has an Euler circuit, it will be drawn in the right window. Try to find the conditions under which we will have an Euler circuit or an Euler path. To draw an edge drag the mouse from the starting vertex to the ending vertex. Repeating that action deletes the edge.

Directed Euler circuits

---

A Hamilton circuit on a graph G is a circuit that visits each vertex of G exactly once. It does not have to use every edge of G. To use the program to get a Hamilton circuit you need to select Properties and Hamilton Circuit. You will see the circuit traced out on the graph.
8. Which of the complete graphs K_n have Hamilton circuits?

9. Which of the platonic graphs have Hamilton circuits?
10. Under what conditions on r and s does the complete bipartite graph Kr,s have a Hamilton circuit? 

    ---

    It can be quite difficult to prove that a graph does not have a Hamilton circuit. For example, try to prove that the Petersen graph does not have a Hamilton circuit. If after 15 minutes you don't have a proof you can look at a proof here. This is not the only proof. You can design your own based on those arguments. 

    ---

    We define a one dimensional cube (the 1-cube) as a graph with two vertices and one edge. Recursively, if you have the (n-1)-cube, you get the n-cube by taking two isomorphic copies of the (n-1)-cube and adding edges between corresponding vertices. Thus the 2-cube is a rectangle, the 3-cube is the usual 3-dimensional cube, and the 4-cube is as shown in figure 18.



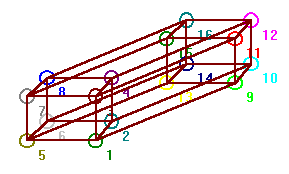
Fig. 18, The 4-cube.


In the program you can get the n-cube by clicking Graph and n-cube.
11. Which of the n-cubes, n=2,3,4,5 have Euler circuits?
12. Which of the n-cubes, n=2,3,4,5 have Hamilton circuits?
13. Which of the n-cubes, n=2,3,4,5 is/are bipartite?

Answers

e-mail: C. Mawata    © C. Mawata