Graph Theory Lessons






 Lesson
20: Spanning Trees
Lesson
20: Spanning Trees

A spanning tree for a connected
graph G is a connected subgraph of G that is a tree
(i.e. has no circuits) and contains all the vertices of G. If G
is a tree then it has only one spanning tree (G itself), otherwise
there will be more than one spanning tree. We will first illustrate a depth
first approach to getting a spanning tree. Get the grid sq5,4.
Now click Find then Spanning Tree and Depth First. You will see
the depth first spanning. You should get a picture like figure 32.

|
|
Fig. 32,
A depth first spanning tree for sq5,4.
|
Click Done so that you get sq5,4
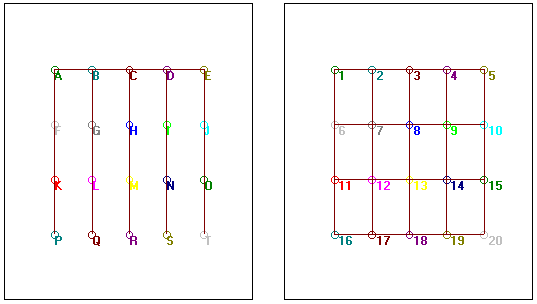
Now find a breadth first spanning tree in the same way you did above. You
should get a graph like Fig. 33
|
|
Fig. 33,
A breadth first spanning tree for sq5,4.
|
-
For the Herschel graph, draw a depth first and a
breadth first spanning tree and then two other spanning trees.
-
Find a graph on five vertices that is not a tree
but such that all of its spanning trees are isomorphic.
-
Which graph is isomorphic to the breadth first spanning
tree of the complete graph Kn?
 e-mail: C.
Mawata
e-mail: C.
Mawata



 © C. Mawata
© C. Mawata


 Lesson
20: Spanning Trees
Lesson
20: Spanning Trees

