Graph Theory Lessons

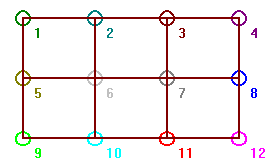
The program allows you to easily draw rectangular and triangular grids. Click Graph and Grids and then Rectangles When asked for the number of vertices across enter 4 and when asked the number of vertices down enter 3. You will get a graph like fig. 31. If m>1 and n>1 we shall call an m by n rectangular grid Sq_m,n.

Fig. 31, The grid Sq4,3.

1. Look at the statistics of a few rectangular grids and find a formula for the number of edges in Sq_m,n. [Hint: How many horizontal edges and how many vertical edges are there?]
2. If m>1 and n>1,
• how many vertices of degree 2 does Sq_m,n have?
• How many vertices of degree 3 does Sq_m,n have?
• How many vertices of degree 4 does Sq_m,n have?
• What is the sum of the degrees of the vertices of Sq_m,n? Does that agree with your answer to question 1?
3. What is the chromatic number of Sq_m,n?
4. If Sq_m,n is regular then what are the possible values of m and n?
5. Find a Hamilton circuit in Sq_4,3 and one in Sq_4,4.
6. If m and n are both odd then Sq_m,n has no Hamilton circuit. You might try to check Sq_3,3 but be warned that it takes a very long time for the program to exhaust all the possibilities and give up trying. To prove that there is no hamilton circuit answer the following questions:
• How many vertices are there in Sq_m,n?
• How many edges will there be in a Hamilton circuit on Sq_m,n?
• Suppose that in a Hamilton circuit you have r right moves, l left moves, u upward moves and d downward moves. How are r and l related and how are u and d related?
• If h is the total number of edges in the hamilton circuit then h=r+l+u+d. Why is this impossible?
7. Clearly Sq_2,2 has an Euler circuit. Is there any other square grid with an Euler circuit? (Sq_1,1 doesn't count!) [ Hint: Use your answer to question 2 .]

   ---

   In the same way as the square grid, you can obtain a triangular grid by choosing Graph then Grids then Triangles. Study the statistics for a few triangular grids.
8. Does a triangular grid always have an Euler circuit? (Why or why not?)

Answers