Graph Theory Lessons

Lesson 3: Isomorphism

Let G₁ and G₁ be two graphs and let f be a function from the vertex set of G₁ to the vertex set of G₂. Suppose that

f is one-to-one and onto
f(v) is adjacent to f(w) in G₂ if and only if v is adjacent to w in G₁.

Then we say that the function f is an isomorphism and that the two graphs G₁ and G₂ are isomorphic. So two graphs G₁ and G₂ are isomorphic if there is a one-to-one correspondence between vertices of G₁ and those of G₂ with the property that if two vertices of G₁ are adjacent then so are their images in G₂. If two graphs are isomorphic then as far as we are concerned they are the same graph though the location of the vertices may be different. To show you how the program can be used to explore isomorphism draw the graph in figure 4 with the program (first get the null graph on four vertices and then use the right mouse to add edges).

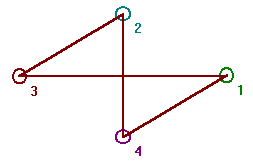
Fig. 4

Save this graph as Graph 1 (you need to click Graph then Save). Now get the circuit graph with 4 vertices. It looks like figure 5, and we shall call it C(4).

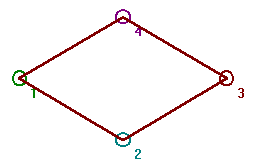
Fig. 5

Click Relations and Isomorphism. You will get a new window with two picture boxes. Click on the Start button. You will get a list of the graphs currently saved. Click on Graph 1. Now the text box should say that Graph 1 and C(4) are isomorphic. Click on Morph. You will get some animation. The graph on the left will deform until it looks like the one on the right. Actually as far as we are concerned they are the same graph. The reason the vertices of the right graph are labeled using letters of the alphabet is so you can talk about them without having duplication of names. In the textbox you will get the relation that connects vertices of one graph to those of the other. If you want to see the animation again click Redo. On these small graphs it only takes a short time to find an isomorphism but on larger graphs it takes much longer. We will discuss this in class in more detail.

When two graphs are isomorphic we consider them to be the same graph. The applet below shows several depictions of the same graph. We shall call it the cube since in one of the depictions it looks like a cube.

Some depictions of the Cube.

When a graph can be drawn without any of the edges crossing we say that it is a planar graph . Fig. 4 and Fig. 5 are the same graph drawn in different ways. Fig. 5 is a plane depiction of it. Of course, not all graphs are planar. To check if a graph's depiction is planar you can click Properties, Planar Graphs, and then Plane?.

Draw all the (non-isomorphic) simple graphs on four vertices.
Let us define a relation R on graphs by G₁R G₂ if G₁ is isomorphic to G₂.

Is R reflexive?
Is R symmetric?
Is R transitive?
Is R an equivalence relation?

Answers

e-mail: C. Mawata