 Graph Theory
Lessons
Graph Theory
Lessons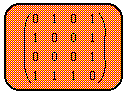



 Lesson
7: Adjacency Matrices
Lesson
7: Adjacency Matrices

The adjacency
matrix of a graph is an n x n matrix A = (ai,j) in which the
entry ai,j =1 if there is an edge from vertex i to vertex
j and is 0 if there is no edge from vertex i to vertex
j. By the way, a matrix with only zeros and ones as entries is called
a (0,1) matrix.
In the applet below draw a few graphs and the applet will display the
adjacency matrix of a graph you draw.
A graph and its adjacency matrix
To use the program Petersen to see the adjacency matrix of a graph, you should first get the program to draw the graph and then
click Properties and then Adjacency Matrix.
-
Look at the adjacency matrix of the null graphs N3,
N10, N15. Describe the adjacency matrix of a
null graph.
-
Look at the adjacency matrix of the complete
graphs K3, K10, K15. Describe the
adjacency matrix of a complete graph.
-
Look at the adjacency matrices of a few more graphs.
Give an interpretation for the sum of the entries in row i of an
adjacency matrix.
-
Suppose you are told that the adjacency matrix for a simple
graph has 5 rows and 5 columns. Suppose you are also told that each row contains three
ones and two zeros, why is this impossible?
-
Get the adjacency matrix for a cube. It should look
like figure 10

|
|
Fig. 10, The cube and its adjacency matrix
|
Now click Edit and then Swap labels.
When you get the prompt "Enter first label" enter 3 and when it
says "Enter second label" enter 7. You will see the graph re-drawn
with the vertex labels 3 and 7 interchanged. Of course it is the same graph;
only the names of the vertices are changed. Now look at the adjacency matrix
again. Write it down and compare it to figure 10. What changes have occurred
in the matrix? Notice that the adjacency matrix depends on how we choose
to label the vertices of the graph.
Recall from your algebra classes that you can (sometimes)
multiply matrices together. When you multiply an adjacency matrix A by
itself you get a new matrix A². Remember that if A is an n x n matrix
and B=A² then the entries bij of B are obtained as
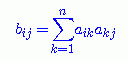 .
.
Therefore bij=1 if and only if there is a vertex k with
aik=1 and akj=1. Well this is the same as saying
that there is a path of length 2 from vertex i to vertex j. So we can conclude
that bij is the number of paths of length 2 from i to j. (If
i=j then you just get the degree of the vertex).
-
The trace of a matrix is the sum of the elements
along the main diagonal,
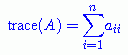 .
.
If a graph has adjacency matrix A, how is the trace of A³ related
to the number of triangles in a graph?[Hint]
 e-mail: C.
Mawata
e-mail: C.
Mawata




© C. Mawata
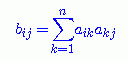 .
.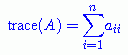 .
.