 Graph Theory Lessons
Graph Theory Lessons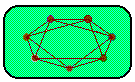



 Lesson
15: Complements
Lesson
15: Complements

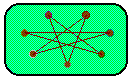
The complement, ~G of a graph G
is a graph with the same vertices as G and with the property that
two vertices in ~G are adjacent if and only if they are not adjacent
in G. If you draw a graph on either side of the following applet it will
construct for you the complement of that graph on the other side. You will find
the picture is less cluttered if use only a few vertices.
A graph and its complement
In the Petersen program if you have a graph and click Operations
and Complement you will get the complement of the graph.
-
What is the complement of the complete
graph Kn?
-
Get the graph of the complete
bipartite graph K2,3 and get the complement. You
should have a graph like figure 23.
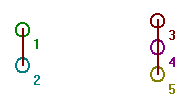
|
|
Fig. 23..
|
Now move vertex 4 by dragging it with the mouse.
You will find that the vertices 4, 5, and 6 form a triangle as in Fig.
24.

|
|
Fig. 24.
|
What is the complement of Kr,s?
(Hint: it is the union of two graphs)
-
What is the complement of the complete
tripartite graph Kr,s,t?
-
If a graph with n vertices is regular
of degree r, is its complement regular and if so of what degree?
[Hint: Experiment with regular graphs like circuits, platonic graphs, the
Petersen graph, n-cubes, complete graphs etc. until you see a pattern]
-
For what value of n greater than 1 is the circuit
Cn isomorphic to its complement?
-
What is the complement of a star
Sn? [Hint: It is the union of two graphs. You might have to move
vertex 1 around so as to see clearly.]
-
Does the complement of the Petersen graph have an
Euler circuit?
-
Suppose a graph G on n vertices, n
odd, has an Euler circuit. Does its complement ~G, if connected,
have an Euler circuit?
-
Suppose a graph G on n vertices, n
even, has an Euler circuit. Does its complement ~G, if connected,
have an Euler circuit?
-
Get the circuit C5; store it as
graph 1. Find its complement ~C5 and store it as graph
2. Now get the star on seven vertices S7, store it as
graph 3 and find its complement ~S7 and store it as graph
4. Now get the union of graphs 2 and 4, i.e. ~C5 U ~S7
and store that as graph 5. Get the sum of graphs 1 and 3, i.e. C5
+ S7, and get its complement ~(C5 + S7).
Store that as graph 6. Now how do the graphs 5 and 6 compare?
-
In general how is ~(G1+G2)
related to ~G1 and ~G2?
 e-mail: C.
Mawata
e-mail: C.
Mawata



 © C. Mawata
© C. Mawata


 Lesson
15: Complements
Lesson
15: Complements

