Graph Theory Lessons

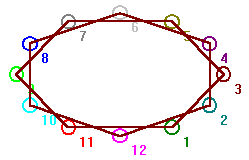
A lace L_n,r, also known as a circus, is a graph on n vertices x₁,x₂,...,x_n, with vertex x_i adjacent to vertex x_j, if j = (i + r) mod n. To see an example in the program click Graph and Lace and L(n,r). When asked for the number n of vertices enter 12 and when asked the value r of the lacing, enter 2. This will give you the graph in figure. 27.

Fig. 27, The lace L12,2.

Fig. 28, The two components of the lace L12,2.

1. How many components do the graphs L_12,1, L_12,2, L_12,3, L_12,4,...,L_12,11 have?
2. How many components do the graphs L_25,15 and L_20,12 have?
3. In general how many components does L_n,m have?
4. How many vertices does each component of L_n,m have?
5. Under what conditions is L_n,m isomorphic to the circuit C(n)? 

   ---

   We can of course lace the graph more than once. The Lace L_n,r,s is a graph on n vertices x₁,x₂,...,x_n, with vertex x_i adjacent to vertex x_j if j = (i + r) mod n or j = (i + s) mod n. To get L_n,r,s the procedure is the same as before except that you choose the option L _n,r,s .
6. How many components will L_n,r,s have? [You will have to do a few experiments before you see a pattern].
7. How many vertices will each component of L_n,r,s have?

Answers