 Graph Theory Lessons
Graph Theory Lessons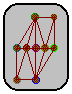



 Lesson
18: Line Graphs
Lesson
18: Line Graphs

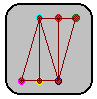
The line graph L(G)
of a graph G is a graph that has a vertex for every edge of G,
and two vertices of L(G) are adjacent if and only if they correspond
to two edges of G with a common end vertex.
If you draw a graph on the left side of the following applet it will
construct for you the line graph of that graph on the other side. You will find
the picture is less cluttered if use only a few vertices and edges.Start with just one edge
before you make the graph more complicated. To help you see which vertex in the
line graph corresponds to an edge in the original the edge and corresponding vertex
are colored the same color.
A graph and its line graph
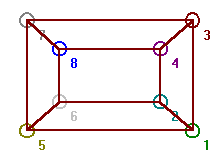
Using the program Petersen you can get some more interesting examples. In the program, get the
graph of a cube (figure 29),
|
|
Fig. 29,
The cube
|
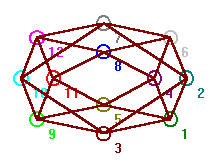
and then click Operations and Line
graph. You will get a graph like figure 30.
|
|
Fig. 30,
The line graph of the cube
|
Notice that the number of vertices in the line
graph is equal to the number of edges in the cube. Vertex 1 in the line
graph corresponds to the edge from vertex 1 to vertex 2 in the cube and
vertex 2 in the line graph represents the edge from 1 to 3 and so on.
A word of warning -- very often you will not be
able to see all the edges as some might be hidden behind others. Get the
graph of K5 and find
its line graph. Now click Properties and Statistics to get
the number of vertices and edges in the line graph. You will find that
there are more edges than seem to be in the picture on the screen. Now
use the mouse to move the vertices a little. You will find that more edges
become visible.
Since we need a non-empty set of vertices for
a graph the line graph of a null graph is undefined. If graphs G1
and G2 are isomorphic
then L(G1) and L(G2) are isomorphic.
However the converse is not true.
-
Find two graphs G1 and G2
which are not isomorphic but for which L(G1) and L(G2)
are isomorphic. [Hint: try a star and a
circuit].
-
Give an example of a graph that is isomorphic to
its line graph.
-
If an edge has a vertex of degree d1
at one end and a vertex of degree d2 at the other, what
is the degree of its corresponding vertex in the line graph?
-
Suppose a graph G is regular
of degree r. Is L(G) necessarily a regular graph, and if
so of what degree?
-
Use your answer to question 4 to give a reason why
the line graph of a regular graph, if connected, always has an Euler
circuit.
-
We already know that the complete graph K5 has 5 vertices, that each vertex is of degree 4, so the sum of the degrees of the vertices is 20 and the graph has 10 edges. Use the program to get the same information for L(K5). (Use the statistics menu item;
Don't bother to move the vertices around.)
-
How many edges and how many vertices does L(L(K5))
have?
-
How many edges and
how many vertices will L(L(L(K5))) have? (your program
won't do this as there are too many vertices for it to handle)
-
Look at the line graphs of a few stars and decide
what L(Sn) is.
-
Prove that if a graph G contains a vertex
of degree d then L(G) has chromatic number greater than or
equal to d. [Hint: use your answer to question 9] .
-
Suppose the sum of the degrees of a graph is 16.
How many vertices does its line graph have?
-
Suppose the sum of the degrees of a graph is s.
How many vertices does its line graph have?
-
Which platonic
graph is isomorphic to the line graph of K4?
Sometimes people consider the problem of coloring
the edges of a graph in such a way that edges that have an end vertex in
common do not have the same color. Such a problem is equivalent to doing
a vertex coloring of the type we did except that it is now done to the
line graph.
 e-mail: C.
Mawata
e-mail: C.
Mawata



 © C. Mawata
© C. Mawata


 Lesson
18: Line Graphs
Lesson
18: Line Graphs

